Differences between Standard Deviation and Variance
Contents
Differences between standard deviation and variance
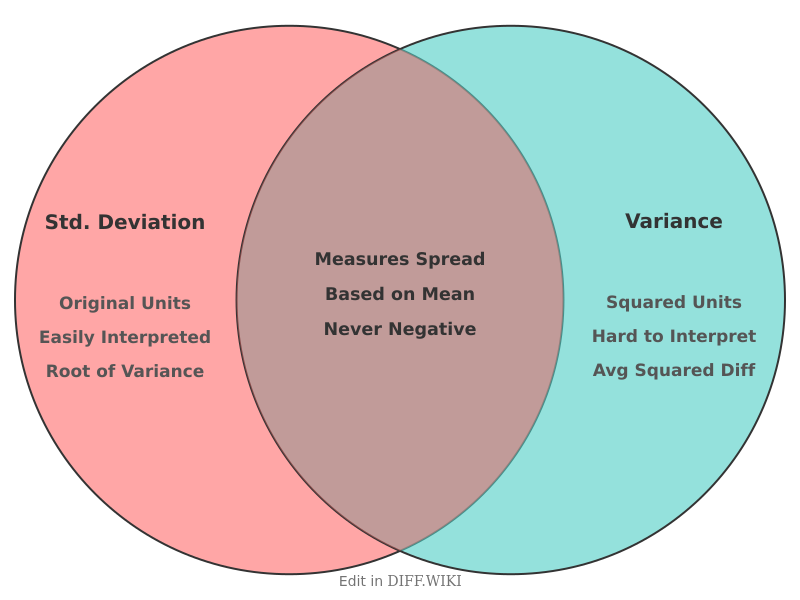
In statistics, standard deviation and variance are two foundational measures of dispersion, quantifying how spread out the values in a data set are from their mean.[1] Variance is defined as the average of the squared differences from the mean.[2][3] The standard deviation is the square root of the variance, a calculation that returns the measure to the same unit of measurement as the original data.[1][4] A low standard deviation or variance indicates that data points are clustered tightly around the mean, while a high value indicates they are more spread out.[5]
Comparison table
[3]| Interpretation| Category | Standard deviation | Variance |
|---|---|---|
| Definition | A measure of the amount of variation or dispersion of a set of values.[1] | The average of the squared differences from the mean.[3] |
| Calculation | The square root of the variance.[3] | The average of the squared differences of each data point from the mean. |
| Symbol | σ (for a population) or s (for a sample).
[1]| σ² (for a population) or s² (for a sample). | |
| Units | Expressed in the same units as the original data. | Expressed[2][1] in the square of the units of the original data. |
| More intuitive for describing the spread of data because its units match the data. | Less intuitive for direct interpretation due to squared units. | |
| Common usage | Frequently used in descriptive statistics to summarize the spread of data. | Used in inferential statistics and theoretical probability, such as in the analysis of variance (ANOVA). |
Interpretation and usage
The primary practical difference between the two measures lies in their units. The standard deviation is expressed in the same units as the data itself, which makes it more directly interpretable. For[2] example, if a dataset measures heights in centimeters, the standard deviation will also be in centimeters, allowing for a direct comparison to the mean height.
In contrast, the variance would be expressed in square centimeters, a unit that is not practically useful for describing the typical deviation from the average height. This[3] use of squared units can make the variance difficult to understand in a practical sense.
Despite this difficulty in direct interpretation, variance is a key concept in statistical theory and is used in further calculations. Squaring the deviations from the mean ensures that all values are positive, preventing negative and positive deviations from canceling each other out. This property makes variance mathematically tractable and foundational to statistical tests like ANOVA and in regression analysis. The standard deviation is then calculated from the variance to provide a more intuitively useful measure of dispersion.[3]
References
- ↑ 1.0 1.1 1.2 1.3 1.4 "wikipedia.org". Retrieved February 02, 2026.
- ↑ 2.0 2.1 2.2 "wikipedia.org". Retrieved February 02, 2026.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 "scribbr.com". Retrieved February 02, 2026.
- ↑ "mathsisfun.com". Retrieved February 02, 2026.
- ↑ "investopedia.com". Retrieved February 02, 2026.